1. The Dawn of Economic
The well-known novelist Robert Louis Stevenson famously observed, “To be idle requires a strong sense of identity,” emphasizing the need for a distinct identity in order for anything to really exist and flourish. This idea encompasses all facets of life, including economics, which is becoming a more important discipline in modern society due to its useful applications and substantial gains in human welfare. Although it is now very popular, economics used to have trouble defining itself and was frequently seen as just another branch of political science or philosophy.
Economics was not entirely an academic discipline from the outset. It was categorized as sociology and lacked a distinct identity. In the late 19th and early 20th centuries, sociology and economics emerged as separate academic fields, primarily due to the differences in the order of analysis: sociology assesses individual behavior by looking at the patterns of group behavior, whereas economics analyzes human behaviors by building upon the analysis of individual behavior. Economist Gary Becker made a great contribution to this transition process of economics by separating economics from methodology and suggested the “Econ approach to human behavior.” Gary Becker was a renowned American economist who extended the scope of economic analysis to a wide range of human behaviors and social issues traditionally considered outside the purview of economics.
2. Gary Becker and the Economics Approach to Human Behavior
By approaching analysis from a personal perspective, Gary Becker set economics apart from the “social sciences” and proposed the idea of an “economics approach to human behavior.” Five constructive assumptions form his theory:
a. “Scarcity of resources exists:” This is often heard as the basic principle or purpose of economics— to distribute and allocate limited resources. In terms of a utility function, which will be mentioned later, scarcity is represented by the budget constraint proportions.
b. “Stable preference: ” For the convenience of economic assumptions, it is assumed that humans have certain tangible objectives (e.g. to earn money, to have a lovely family, etc) and that the objectives are consistent or that they would not vary by time. A stable preference enables economists to develop a utility function that is constructed with numbers.
c. “Purposive behavior/ maximizing behavior:” People make decisions based on their preferences and limitations in order to maximize their level of satisfaction, or in technical terms, utility. In terms of the utility function, it would be expressed in the way of max u{x, y, …}
d. “Equilibrium:” According to Becker’s equilibrium assumption, people modify their behavior in social situations or competitive markets until they believe that making no more changes would improve their situation in light of their goals and the information at hand. As a result, there is no longer any motivation for people to alter their behavior. It can also be implied, in terms of group-level equilibrium, that both sides of a cooperative action have to be satisfied. For instance, nash equilibrium in game theory.
e. “Empirical verification/ causal inference:” This might not be the most essential part of Gary Becker’s assumption of human behavior, but an evaluation of the authenticity of an economics theory is needed through either lab or field experiments.
3. Scarcity/ Constraints
To understand a budget constraint graph, let’s first set the variables:
- Px, Py: the price of a single item x or y
- X, y: quantity of item purchased
- M: the total budget
- Assume that x>=0, y >= 0
The budget constraint function would be:
PxX+PyY=m
Now, let’s construct a budget constraint graph with quantities x and y, respectively, on the x-axis and y-axis.
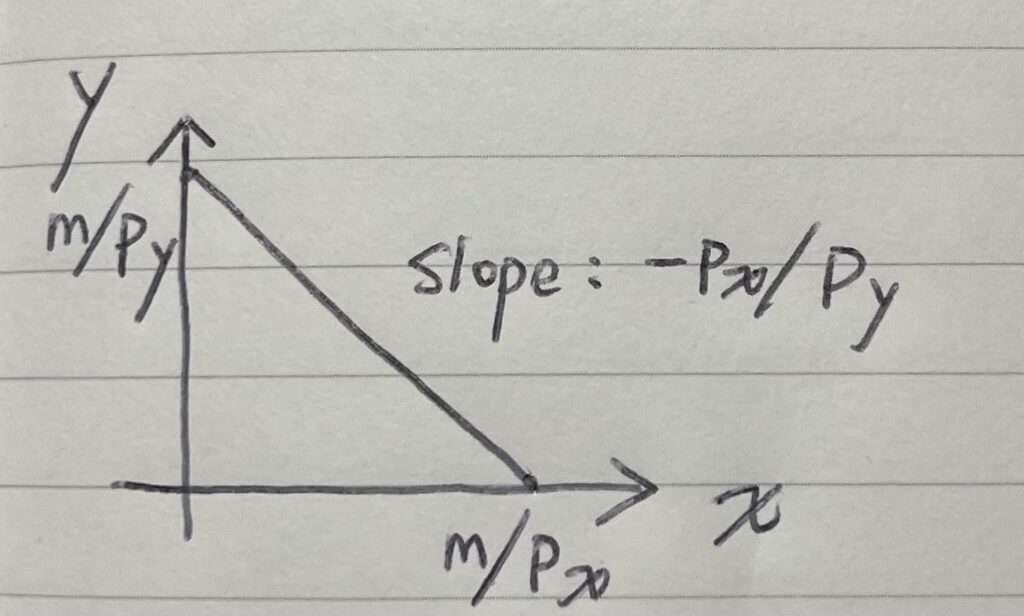
a. To acquire the numeral traits of this graph
- Px/X+Py/Y=m
- PxX/Py+y=m/Py (divide both sides by Py)
- y=m/Py-PxX/Py = (-Px/Py)+m/Py
Just like a linear function y=ax+b, (-Px/Py) corresponds to the slope of the function while m/Py corresponds to the y-intercept. Setting y to 0 concludes us that the x-intercept is m/Px
b. Interpretation of these traits
- Intercepts: The intercepts m/Py and m/Px symbolize the quantity of items that we could purchase within this budget constraint if we only purchase one of them.
- Slope: The slope (Px/Py = ($/unit X)/($/unit Y)) symbolizes a nominal sacrifice or monetary sacrifice: with one more/less unit of money spent on item X sacrifices a unit of money spent on item Y. Or this monetary relationship can also be translated into a real sacrifice, or a sacrifice in quantity (simply unit Y/ unit X): an extra unit of purchase on item Y sacrifices a unit of purchase of item X. In other words, the ratio of the prices of the two goods equals the ratio of the quantities purchased at the optimal consumption point because this is where the consumer’s marginal rate of substitution equals the market’s rate of substitution, and that is why the nominal sacrifice ratio can be translated such smoothly into a real sacrifice fraction.
4. Indifference Curve
- Significance: An indifference curve can be added to the previously mentioned budget constraint graph. It shows the preferences of the consumer and the compromises they are ready to make when choosing between two different combinations of products or services. An indifference curve that has been integrated into the budget constraint line is shown below.
- Interpretation of Graph:
- Concave/ convex: The curving direction of a budget constraint graph depends on the kind of products X and Y are. If they are perfect substitutes, then the budget constraint curve could be simply straight. If goods X and Y are perfect complements, the budget constraint will be an L-shaped curve. This means the goods are always consumed in fixed proportions, and the consumer derives no additional utility from having more of one good without the other. In other cases, indifference curves are mostly in the form of a convex curve, symbolizing the preference for variety (in other words, the average is better than the extreme).
- How curved indifference curves are: the more flat, the more flexible, the more right-angled, the more rigid the selection is
- The steepness of the slope: Symbolizes the willingness to pay for one of the items. If the slope is steep (if the definite value of the slope is greater than 1), it means that the consumer is more willing to give up Y to get X. On the contrary, if the slope is flat (the definite value of the slope is less than 1), it means that the consumer values Y item more.
- Monoticity: The more the quantity, the better the choice. The goals of the consumer are achieved by anything that falls on the indifference curve, or as we see on the graph, the intercept of the budget constraint and the indifference curve. Nevertheless, items on the upper right side of the curve provide greater utility, whereas items on the lower left side of the curve are not satisfying.
- No framing: If X and Y are perfect substitutes for eachother, then two selections, such as (a, b) and (b, a), should not be different from each other.
