Prisoner’s Dilemma in Real-Life Situations: Collusion Models and Price Stability

Runyu Zhao^1*, Minjun Xiao^1**, Leyan Liu^1***

^1* St. Mark’s School, Southborough, United States, 01772

^1** International Business School, Hunan University of Technology and Business, Changsha, China, 410205

^1*** Changjun Senior High School International Department, Changsha, China, 410000

Corresponding author: Runyu Zhao, Email address: runyuzhao@stmarksschool.org

ABSTRACT

With the advance of the market economy, market equilibrium is confronted with a challenge. How to maximize revenue is the maximal conundrum for every enterprise. In this paper, the difficulties of finding a better payoff condition in the Prisoner’s Dilemma model, a classic game theory concept, are demonstrated by simulating the duopoly competition between Pepsi and Coke. The presence of collusion is explained in light of this situation’s advantages for businesses as well as its significant negative effects on society at large. Meanwhile, a method for price stabilization is put out to revise the guidelines for company pricing changes and prevent collusion in particular ways.

Keywords: Prisoner’s dilemma, game theory, duopoly, collusion, price stability

1. INTRODUCTION

1.1 Literature Review

In game theory, the Prisoner’s Dilemma is a common illustration of a non-zero-sum game in which an individual’s best decision is not necessarily the best decision for the group. Alternatively, group decisions made by reasonable individuals frequently result in collective irrationality [1].  Despite this, the typical Prisoner’s Dilemma is set up in such a way that both parties choose to protect themselves at the expense of the other participant. As a result, both participants find themselves in a worse state than if they had cooperated with each other in the decision-making process. The Prisoner’s Dilemma is one of the most well-known and researched concepts in modern game theory [2].

In a Prisoner’s Dilemma setup, the term “Nash Equilibrium” is a definition for the payoff combination of the two participant’s respective best responses for different situations. When excluding the factor of penalty in the game, the Nash Equilibrium a Prisoner’s Dilemma concept is not socially efficient [3] since mutual consent is hard to reach because of the conflicting incentives that each participant faces. The difficulty in getting mutual consent in the Prisoner’s Dilemma demonstrates the challenges of cooperation when self-interest and uncertainty are involved.

However, by merely including one feature—allowing the two players to collude—the problem of not being able to achieve the maximum mutual advantage can be resolved. The two parties would be able to focus their actions on obtaining the highest mutual payoff by building a system of trust. In reality, the colluding parties may collectively choose to influence the market supply of a good or agree to a specific pricing level which will help the partners maximize their profits to the detriment of other competitors. It is common among duopolies [4]. Collusion, which is defined by law as an illegal behavior, is seen to have a detrimental effect on consumer welfare and the economy. Specifically, this results in a reduction in consumer surplus and allocative inefficiency (Price is raised above marginal cost) [5], and therefore collusion is mainly regulated by governments. Using game theory models for detection, government officials might carry out tasks that could avert collusion [6], offering penalties to collusion participants, and setting rules in the game to limit cooperation. When the factor punishment (penalty from the government) is incorporated into the game model, the payoff set for cooperation between both sides is reduced.

1.2 Overview of Pepsi and Coke’s Conditions

According to Brand Finance, Coca-Cola has a market cap of $279.653 billion, while Pepsi has a market cap of $235.6 billion. Interestingly, over the past 12 months, shares of both “Coke” companies have risen 14.5%. According to Euromonitor, Coca-Cola will hold 14.9% of the global soft drinks market in 2020, while PepsiCo will hold 7.2%. This situation is consistent with our predicted results, and the two enterprises are presumably to be connected to achieve the purpose of profit.

However, seeing our model cannot be tested empirically, the model in this paper is based on game theory and related theories. Whereas we will give the most reasonable research results according to the existing conditions. The paper will be discussing the following context—first, how the mechanism of collusion operates. Then the methods authorities would perform to reject collisions.

2.  ANALYSIS OF COLLUSION AND PRICE IN GAME THEORY

2.1 Basis Theory of Prisoner’s Dilemma

The classic Prisoner’s Dilemma is presented as Two members of a criminal gang being arrested and imprisoned by the police. They were held in separate and solitary cells and had no way of contacting each other. Prosecutors lacked enough evidence to convict both men on the main charges, but they had enough evidence to convict both men on lesser charges. Simultaneously, the prosecutor offered each prisoner a deal. Each prisoner was given the opportunity to betray another, to prove that another had committed a crime, or to remain silent and cooperate with the other.

The basic Prisoner’s Dilemma game matrix is constructed in Table 1:

Table 1. Basic Prisoner’s Dilemma Game Matrix ^[1]

The phrases “cooperate” and “defect” relate to the suspects working together (for instance, if neither confesses) or defecting (for instance, when one suspect confesses while the other does not) with one another) [1]. In cells (a) through (d), the first numeral displays the reward for Suspect A, whereas the second numeral displays it for Suspect B [1]. As the table infers, if either player selects to defect, they will either receive a -2 payoff or get the maximum 0 payoff. However, if they choose to cooperate, they either get a -1 or -3 payoff. Clearly, the best strategy for A and B, respectively, is to defect, regardless of what the other player does. Nash Equilibrium, being the circumstance where neither of the suspects would benefit from a unilateral deviation, is when both suspects defect instead of cooperating [7].

In terms of this model’s economic significance, the payoff values (-1, 0, -3) in the matrix represent the economic outcomes for each combination of choices. First of all, the temptation to betray symbols is a substantial detriment, indicating a strong incentive for a player to defect when the other cooperates. It reflects the economic advantage or reward associated with choosing defection over cooperation or attempting to maximize personal benefits rather than mutual benefits. It demonstrates the allure of short-term gains even at the expense of mutual collaboration. Secondly, the punishment for both players defecting is more severe than the one for mutual cooperation. It emphasizes the economic cost of detriment with damage to economic interest related to mutual trust. The sucker’s payoff (-3) represents the cost incurred by a player that chooses to cooperate when the other chooses to defect. It signifies how susceptible to exploitation cooperative individuals are. The economic significance lies in understanding the potential economic losses associated with trusting behavior in the face of betrayal.

2.2 Case Study

2.2.1 Profits Analysis under Non-collusion Conditions

Now, simulating this situation with a realistic example would be more explicit. Set Coca-Cola and PepsiCo as the primary players in this game. In this duopoly market, Coca-Cola and PepsiCo often compete head-to-head in various markets around the world. Their products are quite similar in terms of taste and composition, and consumers might not be able to easily distinguish between the two based solely on product attributes. The fact that customers can readily select the provider with the considerably lower price demonstrates that the two companies co-exist in a highly elastic market that is sensitive to price changes (a minor change in pricing can result in a significant difference in the quantity demanded) [8].

We consider a simple model for two players (Coco-Cola and Pepsi), where these companies engage in intense competition. Consider the following demand functions where demand for each company depends on the prices of its own product and competitors. Demand Di for the provider is given by:

D1=D01-b1P1+β1P2                                   (1)

D2=D02-b2P2+β2P1                                   (2)

And total demand for the market is

In the above simple demand model, we assume the two companies don’t engage in collusion, then each company will set a price level in (1) and (2) to maximize its profit while the other company’s price is taken as fixed (exogenous factor), i.e.,

Max (PiDi-Costi), i=1,2

Here if we assume the two companies’ products are highly identical as nearly perfect substitutes’ demand price elasticity is very high, and the two companies don’t engage in collusion, then it’s obvious that each company will benefit by setting its price just below its competitor’s level if not lower than its cost to take all its competitor’s customers. The result can be very close to what is derived from a standard competition model, where each company sets its price at its cost, which implies maximal social benefit but zero profit for individual companies.

2.2.2. Profits Analysis under Collusion Conditions

In the Collusion case where two companies have the possibility of jointly setting up their strategies for maximal benefit combined, the two companies will jointly set up P1 and P2 to maximize the profit derived from the total demand function (3).

In normal cases, it is assumed that the impact of the change in a company’s own price (“direct impact”) on its quantity should be no less than that of the change in the other company’s price (“indirect impact”), therefore,

Bi>=βi for i=1,2

Or Bi-βi>=0.

Then in a complete collusion case, the best strategy played by the companies will be derived by

In this case, P1 and Cost1 are related to Coca Cola Co while P2 and Cost 2 are for Pepsi Co.

To simplify the analysis, we assume cost can be insignificant, and the two companies will aim to maximize their combined revenue; we can further assume that the optimal price is the same for the two companies as they produce nearly closely substitutable products, therefore the combined revenue is equal to

 Max (P x（D1+D2）)                       （5）

Then we can find the optimal strategy for the two companies by taking the first-order derivative of (5), and the price will be larger than the result in the non-collusion case in the previous section. We choose not to work further on the calculation based on these models while we want to instead focus on following the more popular and intuitive “Prisoner’s Dilemma” approach.

We use Table 1 below for the analysis. As we mentioned before, as the market is very elastic, a rise in price by a company would cause customers to choose its competitor and result in a significant decrease in the quantity of demand for its own product, which would lead to a decline in overall reward. InMaillé et al’s paper, the loss of overall reward is [9].  On the other hand, a price cut would result in a big rise in the amount of product sold out, increasing Di’s overall income (when profit per unit of product is slightly dropped, but the quantity of demand is highly raised), where ‘bipi’ would be extremely high. In this situation, none of the sides would attempt to increase their pricing in this extremely competitive market. Table 2 below illustrates the payoff combination for the two players with different strategy choices.

Table.2 The profit table for various price-changing conditions

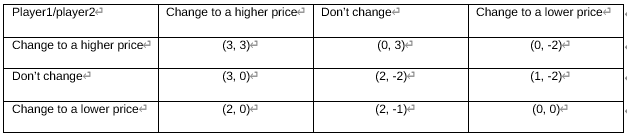
According to Table.2, player 1 and player 2 are more willing to change their price to a higher digit in order to get more profits. However, collusion, an anti-competitive practice intended to prevent direct competition, lessen market uncertainty, and generate higher profits, might change the situation in which two businesses are unable to reach a better mutual benefit [10]. In a duopoly competition model, given the behavior of its rival, each enterprise has its own incentive to increase production or lower prices to achieve a non-cooperative equilibrium. However, economists have long had a hunch that businesses might cooperate repeatedly to increase prices or limit production in order to make more money [11]. The maximization of the shared profit under specific legally binding agreements is in the interest of all participating businesses in enterprise cooperation. Therefore, coopetition is a highly advantageous partnership between rivals in which businesses can provide value, reap financial rewards, and minimize losses[11]. Relating this to Table 2, if Coke and Pepsi agree to raise their prices simultaneously, and if either company complies with the agreement, a particular penalty would be imposed. On the other hand, the side that disobeyed would compensate the company that continued to adhere to the collusion plan.

Hence, as we can conclude from Table 1, both companies have an incentive to play a “higher pricing” strategy for their best interest. Of course, their gain of interest comes at a cost of total social welfare.

Table.3 The profit table after collusion

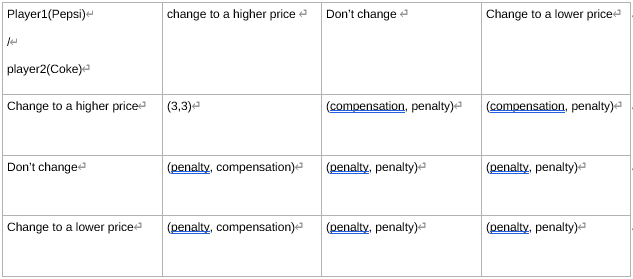
3. DISCUSSION AND CONCLUSION

Collusion is viewed as detrimental to society yet it serves the interests of businesses. Collusion is a type of anti-competitive action that eliminates competition in the market, raising prices and limiting consumer options. Additionally, collusion is preventing new companies from joining the market, which is a major barrier to innovation and growth[11]. Despite this, collusion may result in a market monopoly or duopoly, in which consumers must pay higher prices or purchase lower-quality goods or services. As for the enterprise itself, assume in a duopoly competition model, given the behavior of its rival, each enterprise has its own incentive to increase production or lower prices to achieve a non-cooperative equilibrium. Nevertheless, economists have intuitively known that higher profits can be gained if enterprises repeatedly interact to collude by collectively raising prices or limiting production.

3.1 Defense Mechanism

In this fashion, antitrust groups would modify the game theory scenario’s game rules to include defensive mechanisms. The term “price stability” refers to one of the most well-known defense mechanisms. Instead of every period, suppliers should be permitted to change their prices every k period, where k is the regulator-set stability restriction over time [12]. Price stability is the idea of maintaining prices at roughly the same level over an extended period of time. The purpose of enforcing pricing stability regulations is to deter or prevent providers from abruptly and collectively raising or lowering their prices in an effort to manipulate the market in a way that benefits them all but hurts customers or other competitors [9]. This mechanism can be written formally as follows: for each provider i and each m ∈ N, we impose price stability for a duration of k periods, i.e.

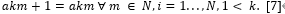
After remodeling the overall utility function [6], the pricing Vi can be expressed as:

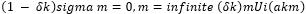
K should be chosen just large enough to prevent collusion.

3.2 Conclusion

Markets that are highly competitive face a serious threat from collusion, but researchers in economics, law, and data analysis have worked together to develop more reliable methods for example Strengthening anti-monopoly and anti-cartel legislation, improving the regulatory system, establishing a competition policy framework, and encourage whistle-blowing and public announcement for detecting and proving collusion. By using detection models with, for instance, the Prisoner’s Dilemma model, authorities can better safeguard fair competition, stabilize the overall price level, protect consumer welfare, and ensure the integrity of markets. The continual fight against collusion highlights the value of alertness, innovation, and a team effort in sustaining wholesome and open market environments as industries and legal frameworks change.

REFERENCES

1. The Prisoner’s Dilemma in Business and the Economy. (2023). Retrieved August 16, 2023, from Investopedia website: https://www.investopedia.com/articles/investing/110513/utilizing-prisoners-dilemma-business-and-economy.asp

2. What Is the Prisoner’s Dilemma and How Does It Work? (2023). Retrieved August 12, 2023, from Investopedia website: https://www.investopedia.com/terms/p/prisoners-dilemma.asp

3. Lehtonen, T. Niṣkāmakarma and the Prisoner’s Dilemma. SOPHIA 60, 457–471 (2021). https://doi.org/10.1007/s11841-020-00780-x

4. Collusion: Explanation, Examples, Preventative Steps. (2023). Retrieved August 11, 2023, from Investopedia website: https://www.investopedia.com/terms/c/collusion.asp

5. ‌‌Phlips, L. (1996). On the detection of collusion and predation. European Economic Review, 40(3-5), 495–510. https://doi.org/10.1016/0014-2921(95)00064-x

6. Gonçalves, M., Wilko Letterie, & Vermeulen, A. J. (2015). Antitrust as Facilitating Factor for Collusion. B E Journal of Economic Analysis & Policy, 15(2), 797–814. https://doi.org/10.1515/bejeap-2014-0023

7. Nash Equilibrium: How It Works in Game Theory, Examples, Plus Prisoner’s Dilemma. (2023). Retrieved August 25, 2023, from Investopedia website: https://www.investopedia.com/terms/n/nash-equilibrium.asp

8. Price Elasticity of Demand Meaning, Types, and Factors That Impact It. (2023). Retrieved August 25, 2023, from Investopedia website: https://www.investopedia.com/terms/p/priceelasticity.asp

9. Maillé, P., Naldi, M., & Tuffin, B. (n.d.). Understanding and Preventing Tacit Collusion among Telecommunication Operators. Retrieved August 16, 2023, from https://hal.science/hal-00447030/file/maille2009understanding.pdf

10. Nasrudin, A. (2020, September 26). Collusion: Meaning, Influencing Factors, Types, Pros and Cons — Penpoin. Retrieved August 17, 2023, from Penpoin. website: https://penpoin.com/collusion/

11. Ding, S., Sun, H., Sun, P., & Han, W. (2022). Dynamic outcome of coopetition duopoly with implicit collusion. Chaos Solitons & Fractals, 160, 112236–112236. https://doi.org/10.1016/j.chaos.2022.112236

12. Importance of price stability. (2012, August 8). Retrieved August 18, 2023, from Eesti Pank website: https://www.eestipank.ee/en/monetary-policy/importance-price-stability